Library Integration for IMU - Computing the Stabilization

 |

|
Introduction
After determining the angular position of the current frame, it is time to determine the distortion angle. The distortion angle represents how much the image deviated from a natural movement (a natural movement has a low frequency). Therefore, the distortion angles often create unwanted high-frequency noise and create waviness in the video.
Stabilization Principle
The RidgeRun Video Stabilization Library computes the distortion based on forward-backward filtering processing using the sleep interpolation between consecutive samples and a smoothing factor. This is known as the Exponential Smoothing[1].
The basic representation of the Exponential Smoothing is given by:
where is the smoothing factor.
The process of smoothing is performed forward in time. Then, using the computed data, it is computed backwards.
Overall, the RidgeRun Stabilization Library requires at least three interpolated samples to perform the stabilization: one from the past, the current, and the following, leading to a non-causal filter. This means that stabilization will introduce a latency of two image frames. As a limitation, the first frame will always be unstabilized, whereas the second frame will be stabilized at the time when the third frame should be processed.
Using the Stabilizers
The stabilizers require a special set of configurations for each algorithm; however, their usage is uniform in terms of the API. Currently, the library contains two algorithms:
- Spherical Exponential: the most basic one.
- Fixed Horizon: an enhanced version of the Spherical Exponential. Similar to the Horizon Lock.
Creating the Settings
Each algorithm has a special set of settings:
Depending on the algorithm, different members must be configured. For instance:
// Smoothing factor: double smoothing = 0.206; auto params = std::make_shared<SphericalExponentialParams>(smoothing);
// Smoothing factor: double smoothing = 0.101; // Angle double angle = M_PI; auto params = std::make_shared<FixedHorizonParams>(); params->smoothing = smoothing; params->horizon_angle = angle;
Creating the Stabilizer Instance
The creation of the stabilizer instance is through the factory available in IStabilizer.
// Assume that the settings match the implementation std::shared_ptr<StabilizerParams> params; // Create the instance auto stabilizer = IStabilizer::Build(kSphericalExponential, params);
In case of providing a wrong set of parameters, it will throw an exception during construction.
Using the Stabilizer
Once created and configured, it is possible to use the Apply() method as in the former algorithms. In this case, the input vector of quaternions must have at least three values: one past sample, the present sample, and a future sample.
// Assume that the interpolation has filled the structure and has three quaternions std::vector<std::pair<Quaternion<Double>, uint64_t>> interpolated; // Correction Quaternion<double> correction; // Apply the correction stabilizer->Apply(correction, interpolated, 0); // Delete the first sample interpolated.erase(interpolated.begin());
The Apply() method do not alter the interpolated. The first sample must be deleted to have room for the following.
Apart from the correction, the quaternion must be rotated (multiply the conjugate of the correction by the current interpolated sample) against the input sample to compute the correction:
// Assume that the interpolation has filled the structure and has two quaternions // The first is already deleted std::vector<std::pair<Quaternion<Double>, uint64_t>> interpolated; // Correction Quaternion<double> correction; // Rotate between: this quaternion can be used by the undistort auto rotated = correction.Conjugate() * interpolated.at(0);
The resulting quaternion is ready to use by the undistort.
Result
Inspecting the result, the interpolated plot is the following:
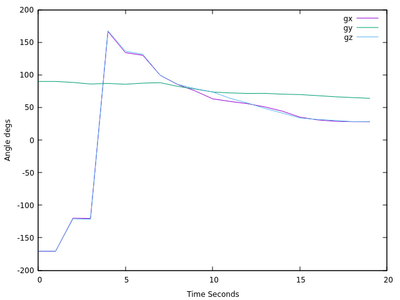
It indicates the position of the system at a given time. The stabilization captures the noise, which is often small angles:
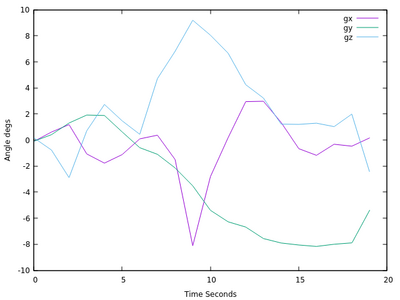
These plots are the result of converting the quaternion to Euler Angles.
- ↑ Exponential Smoothing: https://en.wikipedia.org/wiki/Exponential_smoothing




