Pruning for AI on FPGA
The FPGA Minutes to Become an Expert documentation from RidgeRun is presently being developed. |
| FPGA Minutes to Become an Expert |
|---|

|
| Introduction |
| FPGA Knowledge |
|
Synthesis Flows
|
| Xilinx FPGAs |
|
Evaluation boards Development workflow and tools Getting Started |
| Lattice FPGAs |
|
Evaluation boards |
| Simulation Tools |
| CocoTB |
| AI and Machine Learning |
| Contact Us |
Introduction
Pruning is a model optimization technique that removes weights that do not significantly impact the inference process. It allows for reducing the storage and computations required for the inference tasks. However, it requires specialized data structures and hardware for the computations.
This wiki will explain the sparse data representations, acceleration considerations, and how we can use the FPGA to accelerate sparse operations.
Data Representations
Regarding the data structures, sparse matrix representations are used for matrix computations, encoding the valid rows and columns with a value. However, there are multiple ways to encode the rows, columns, and values:
Coordinate (COO)
It encodes the dense matrices into sparse matrices through three different arrays:
- Row indices
- Column indices
- Values
The three arrays are the same size, and the arrays' positions are accessed using the same index.

So, to access the dense matrix index from a sparse representation, it is possible to use the following pseudocode:
index_1d = rows_indices[i] * leading_dimension + column_indices[i]
Assuming that the indices can be encoded in 16-bit unsigned integers and the values are 32-bit floating points, the number of valid elements to start saving storage is given by:
total_dense_matrix_number_elements >= ((sizeof(indices) * 2 + sizeof(values)) * valid_elements) / sizeof(values)
Not respecting this inequation will lead to suboptimal compression, and the matrix will take more storage than the dense representation. As a rule of thumb, having 50% or fewer valid elements is recommended than the total number of elements of the dense representation.
Compressed Sparse Rows/Columns
These representations compress the arrays of rows or columns to take less space than the previous representation. They encode offsets to reach the index value. They aim to relax the number of valid elements to reach compression, allowing more elements to be compressed.

To compute the dense position, the following expression can be used:
index_1d = row * leading_dimension + column_indices[row_offsets[row] + k]
This representation may lead to complications when determining the matching offset with the column index.
Sliced Ellpack (SELL)
The Sliced Ellpack format is standardized and state-of-the-art. This format allows for significant improvement in the performance of all problems involving low variability in the number of nonzero elements per row.
An MxN sparse matrix A is equivalent to a sliced sparse matrix As with slices = (m/slicesize) slice rows and n columns. Each slice is stored in column-major order to improve memory coalescing and utilization.
The definition of the sparse matrix requires an array of slices, slice size, and number of elements.

The hardware implementation for this representation is reduced in complexity and saves space, given both benefits together.
Hardware Acceleration Minutes
The hardware accelerator design for sparse matrix operations depends on the representation utilized for compressing the sparse representation. In common, they are usually based on operation queues that operate on the matrix elements. In the case of the matrix operations, the accelerator contrasts the operands, seeking valid operations.
Likewise, they are often granular and divided into Processing Elements, allowing processing multiple batches at a time. However, they may require good scheduling to avoid underutilization.
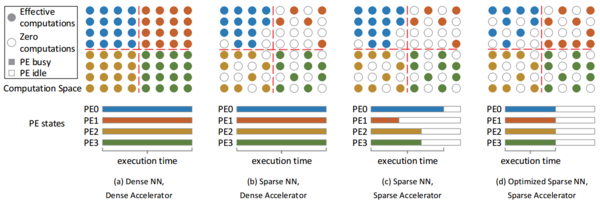
As suggested by Jiajun Li in AdaPrune: An Accelerator-Aware Pruning Technique for Sustainable CNN Accelerators[1], multi-PE sparse accelerators may be suboptimally utilized when the loads are not balanced. Therefore, a good sparse accelerator is usually equipped with front-ends that analyse the operations and schedule the operations into the multiple PEs, optimizing the computing times in exchange for resources utilised for making the accelerator more complex.
In FPGAs, we can create custom architectures that operate on sparse operations and deep learning model pruning artifacts. We can also go further with arbitrary precision and approximate computing operations that help reduce the resource footprint of the accelerators implemented on the FPGA.
- ↑ Li. J. An Accelerator-Aware Pruning Technique for Sustainable CNN Accelerators. Available at: https://ieeexplore.ieee.org/document/9359522



